What is Power Factor (pf)? How high value of pf is benficial in EV charging System?

Power factor correction (PFC) means improving

It is defined as how much active power is drawn from grid in the amount of total power.

In simple terms,

Total Power (S) = Active power (P) + Reactive power (Q)

Total power (S) –> Apparent power = V_rmsI_rms

Active (Real) power (P) –> Useful power = V_rmsI_rms*cos(Φ)

Reactive power (Q) –> Useless = V_rmsI_rms*sin(Φ)

Here,

Power factor = P/S = cos(Φ)

It is defined as ratio of active power to total power

Power factor is high –> Useful / Active / Real power is high

Power factor is low –> Reactive / Useless power is high

Where,

Φ is the phase angle between the voltage and current (deg.)

1. Maximum value –> 1 @ Φ = 0
2. Minimum value –> 0 @ Φ = 90^o

Examples:

• Resistive Circuit

Connected load to the grid is pure resistive nature, See below Fig.

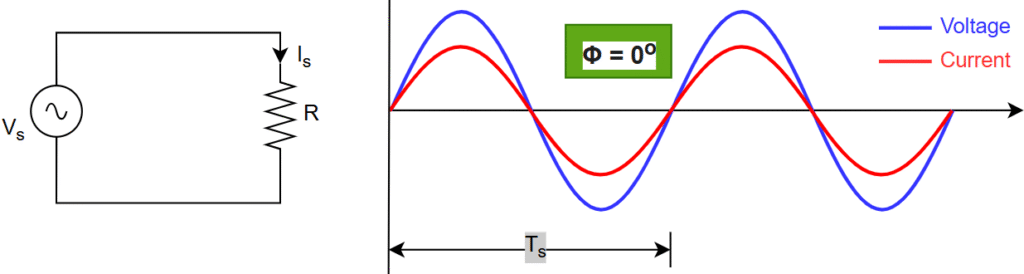
The current drawn is in-phase with the voltage –> Φ = 0 –> pf = 1 –> S = P

Total power (S) = Active power (P)

• Inductive Circuit

Connected load to the grid is pure inductive nature, See below Fig.

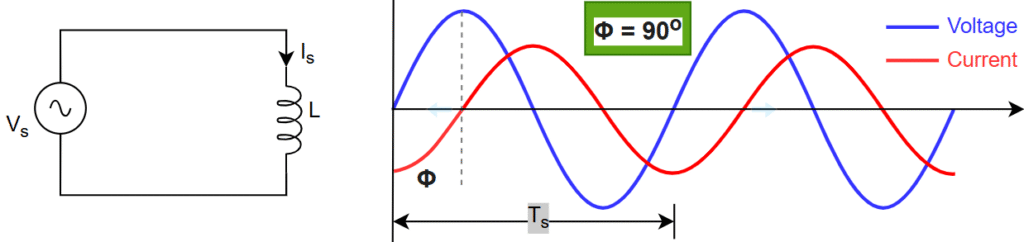
The drawing current is lags with the voltage –> Φ = 90^o –> pf = 0 –> S = Q

The average of active power is “ZERO”

Total power (S) = Reactive power (Q)

• Capacitive Circuit

Connected load to the grid is pure capacitive nature, See below Fig.

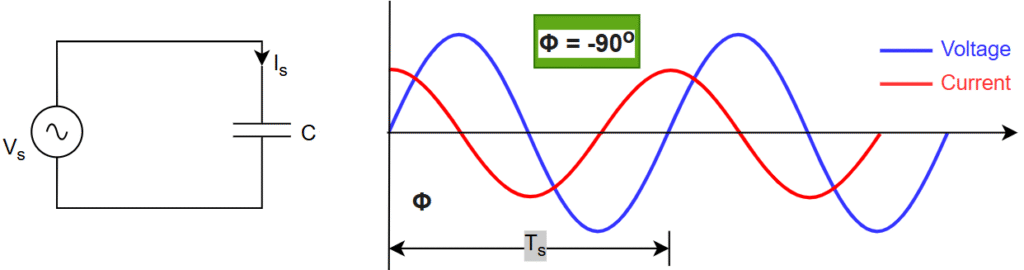
The drawing current is leads with the voltage –> Φ = -90^o –> pf = 0 –> S = Q

The average of active power is “ZERO”

Total power (S) = Reactive power (Q)

Conclusions:

1. Power factor : P/S
2. Power factor value range : 0 to 1
3. Power factor is directly proportional to active power
4. Pure inductive / capacitive circuit power factor is ‘0’, and its average active power is ZERO